「割引率」についてわかりづらい人向けの説明

「割引率」という概念が金融にあります。今の価値と将来の価値は一致しないということですが、考え方や計算方法が少しわかりづらい、理解しづらいという方に向けて、なるべく簡単に説明してみます。個人的には最初に難しい数式が出てくると理解しづらいと思い、極端な話から説明しました。

計算方法だけ知りたい人は目次からスキップしてください。

割引率・割引現在価値とは？どういう意味？計算方法は？

まず非常にざっくりと説明します。

今持っている財産やお金が将来にどのくらいの価値を持つか。ということがメインの考え方です。

ということを考えるとき、今の100円の価値が将来200円なら、これは将来価値200円

逆に将来の200円が現在に直すと100円にあたるなら、現在価値200円

となります。この場合、200円と100円には差があるので、期間で割った場合の平均の変化率を割引率と言います。

一つづつ説明していきます。

割引率とは何か？わかりやすくするために

まずは細かい議論を除いて極端な例で考えてみます。

こいぬさんには100円をあげます。

ひよこさんには200円をあげます。

こいぬさんには「今日」100円をあげます。

ひよこさんには「明日」200円をあげます。

今、りんごが100円で売っています。

ところが、明日からはリンゴが値上がりし1個200円になるようです。

こうなると、こいぬさんとひよこさんのもらった100円と200円というのはどちらも同じ価値＝リンゴ1個分ということになります。

この考え方が非常に大事になります。

お金というものは常に一定の価値があるのではなく、外部要因によってその価値がかあるということです。

ここからは割引率について「金利」とセットで考えていきます。

金利やインフレを含めた割引率、現在価値、将来価値を単純な例で

こいぬさんには100円をあげます。

ひよこさんには200円をあげます。

こいぬさんには「今日」100円をあげます。

ひよこさんには「来年」200円をあげます。

今、りんごが100円で売っています。

ここまではほぼ一緒です。

ここから金利の概念を入れます。

銀行に預けると、来年でお金が2倍になるとします。

この場合も、こいぬさんとひよこさんのもらった100円と200円というのはどちらも同じ価値＝リンゴ1個分ということになります。

実際は金利が年+100%などということは考えられませんがこの場合、ひよこさんのもらう200円の現在価値は100円になるということです。

つまり、金利×年数分お金が増える（減る）のであれば、その分を割り引いて考えるというのが割引率の計算方法です。

割引率の正式な計算方法とは。

正式な計算式と定義は以下です。

割引率とは、将来受け取る金銭を現在価値に割り引く（換算する）ときの割合を、1年あたりの割合で示したもの。

N年後に受け取る現金（C）の現在価値（PV）と割引率（r）の関係は、以下の式で表される。

PV ＝ C ÷　(1＋r)n

https://mba.globis.ac.jp/about_mba/glossary/detail-12118.htmlより

この場合、

PV現在価値＝２００円÷（１+１）¹となり

１００円になります。

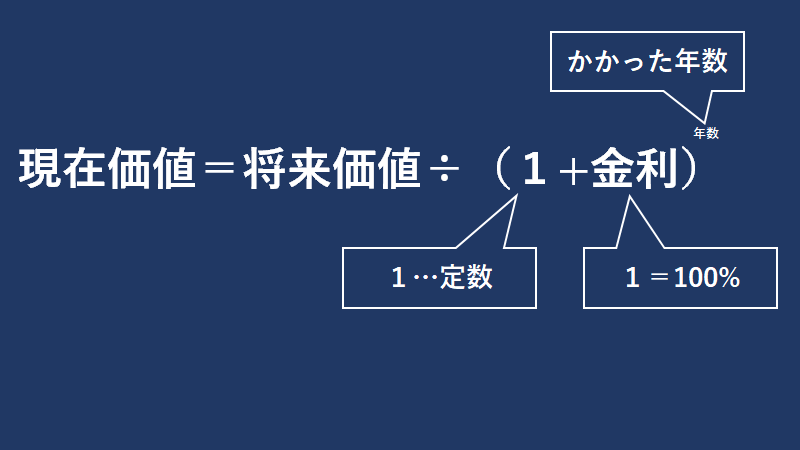
ではこれがもう少しあり得そうな、金利4%とした場合の30年後の200円の現在価値はどうなるかというと

現在価値＝２００（円）÷（1+０．04）³⁰となり、約61．66円になります。

年間4%増やせる前提であれば、将来の200円というのは今の62円弱、1/3未満の価値になってしまうということです。

こうなると、将来の200円というのは現代に直すと200円の価値はない事になります。

このばあい、「価値は1年毎に4%ずつ減っていくから」と言い換えることもできます。

この4%分が「割引率」です。

ここでは「金利」を入れて計算しましたが、将来もらえるお金の不確実性やインフレ・デフレなどを数値化するなどほかにも応用が出来ます。

割引率が理解できなくても知っておきたい、現代価値と将来価値の違い

現代の価値と将来の価値は異なるという点は知っておくべきです。

たとえば投資をすればお金が増えるかもしれません。そういった前提の場合、今のお金の価値は将来の同額より価値の高いものになります。

逆に投資でお金を増やす機会がある場合、将来の得られるお金は現代に置き換えるとより少額ということになります。

また、インフレであれば同額のお金の現在価値＞将来価値となり

デフレの場合は現在価値＜将来価値となります。